Hi again everybody!
Well, so the time has come to what is probably going to turn out as the longest and
most complicated tutorial of them all in the PxdScript series.
Today we are going to finish the first major task in the compilers front-end we are
going to parse the program from the source file and represent it as an AST (remember
what this is from chapter 1? AST is short for Abstract Syntax Tree and is a tree-like
representation of the program but more on this later.)
We need the program in an AST before we can really begin to analyze in the later chapters.
To check that we have parsed the program correctly into the AST well also build a
so-called "pretty-printer" which simply writes the AST to the screen as source code
again. If we parsed the program correctly then the pretty-printer should output something
very similar to the original program file.
Finally we are going to put together what we have learned in chapter 1 to 3 and build
the first executable version of our compiler.
So what exactly does a parser do? Well, remember last time we finished the chapter with a description of which illegal programs our compiler could reject based solely on the scanner. It wasnt hard to find illegal programs which our compiler accepted the example I presented was:
program int foobar = 5 < 8;
So lets take a step back and try to figure out what exactly the problem is with the
line above. We quickly realize that while all the tokens in the line are correct
and legal tokens from our programming language the order in which they appear
is totally wrong.
The parsers job is to reject programs in which some tokens appear in illegal order.
To find out whether or not a given bunch of tokens are in the right order we must
define some sort of grammar, which the programming language must follow.
A grammar for a programming language is called a "context-free grammar" and
its syntax is fairly simple. It is based on a set of so-called "production rules",
which are easier to explain after seeing an example. Below are the production rules
of a very simple mini programming language:
As you can see I have defined a number of symbols above. The symbols which appears on the left side on some production rule are called nonterminals while the symbols which only appears on the right hand sides are called terminals. You can then think of the production rules as ways to expand a nonterminal into something else, possibly including terminal symbols. The terminal symbols are the tokens from our programming language and in the example above the terminal symbols is the set
terminals = {;, +, id, num}
and the nonterminals are defined by the set
nonterminals = { S, E }
So what does the rules say in words? Rules 1 and 2 says that the nonterminal S can
expand into either a sequence (rule 1) or an assignment of an E to an identifier (rule
2). Rules 3 to 5 say that E is either an identifier, a numeric constant or a sum of
two other Es. One is free to chose whatever names one likes for the nonterminals in
the productions - they can be thought of as a kind of variables. The names I have
chosen are not totally arbitrary though - S is short for statement and E is short
for expression. These two abstractions (a statement and an expression) is something
we'll meet again later.
Finally we must always define a nonterminal to be the start symbol in
the language above we chose S.
Now we have a way to check if a given string is in our programming languages grammar
or not. The string is legal if we can start with the start symbol defined above
and derive the string using rules from the grammar. Lets take a look
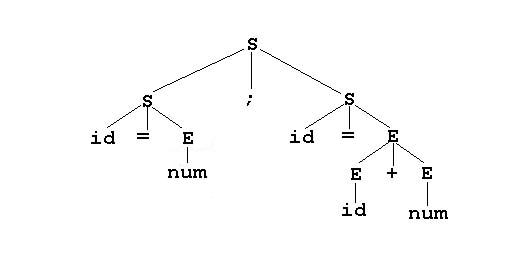
at some examples. Is the string:
'id = num ; id = id + num
a valid string in our example programming language? Well, it is if we can derive it from S using the rules so lets try that.
So by using the production rules 7 times we have derived the string from the start
symbol and thus we conclude that the string is indeed in our program language.
Notice that the tokens in the string match very nicely what our lexer gives us from
a source file the string above could for example have been:
a = 5; b = a + 7
after it had been through the lexical analysis and converted to tokens.
There are a couple of other very important observations to make about this derivation.
First of all it should be clear that one could have derived the string in many other
ways! The first step was pretty obviously but in step 2 I made a choice whether to
start expanding the left or the right side of the sequence. I ended up choosing the
left side but I could just as easily have chosen to expand the right side first.
Secondly notice that the derivation could have gone wrong in many places if I hadnt
made the right choices about which rules to use. One example is in step 5 where I
chose to expand E to E + E. Had I chosen another rule for example to expand E to num
by rule 4 then I would not have been able to successfully derive the string.
And yes, the process of deriving a string is non-deterministic which
is generally a very bad thing for an algorithm, if we wishes to have a machine execute
it for us. We cannot rely on the machine making the right decisions each time!
As it turns out there is a solution (of course) but it is not trivial at all!
Fortunately we dont have to worry too much about it because like scanning, parsing
is something you dont do manually these days we have tools, which will automatically
create a parser for us given the grammar for our language. The tool we will use is
called bison and works in tight cooperation with flex which I introduced
in the last chapter.
There is however still some issues which must be discussed before we can start writing
the bison file for our programming language: PxdScript.
A parse tree is created by connecting each symbol in a derivation with the nonterminal,
which it was derived from. The root node is the start symbol.
For example lets look at the parse tree for the string we derived above.

Notice that if we read the leaves left to right in the tree then we have the string
we derived.
A grammar is said to be ambiguous if it can derive a string in the language
with two different parse trees. It is not hard to realize that the mini-grammar that
I presented above is ambiguous we can create two different parse trees for the string:
id = id + id + id
which obviously is in the language. The two trees are:
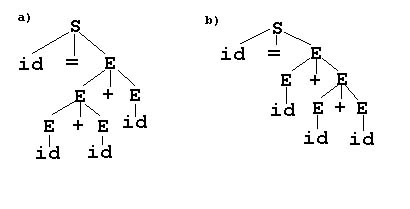
Now, our goal with the parse tree is to have it represent the meaning of the program as well as deciding whether or not it is in the language. So it is obvious to consider the branching as some way of placing parentheses in the expression. We would then expect the two trees to represent the following interpretations:
a) id = (id + id) + id
b) id = id + (id + id)
Now in this particular case where the operator is + it doesnt matter which interpretation is chosen but had the operator been - we would have serious problems:
a) id = (5 2) 6 = -3
b) id = 5 (2 - 6) = 9
The derivation chosen would decide the meaning of our program!
Ambiguous grammars are a problem for parsers and will not be accepted by the bison
tool. This is not really a big loss though as programming languages with ambiguous
grammars wouldnt be very practical to work with anyway.
Fortunately many ambiguous grammars can be rewritten to un-ambiguous ones by introducing
more different nonterminals. Also, fortunately, this is not something we will have
to do manually - bison can handle this for us with a little help (which Ill explain
later).
However before we can give bison that help we must think a little more about the problem.
What can we do to produce the right parse trees each time? Well, the first idea when
one looks at the expression with - above is to say that we always associate
parentheses to the left, favoring the a) version of the tree. This would certainly
work for expressions only including one operator (and produce correct results both
for - and / check it).
But what if we added some more productions to the language to allow E to expand to
both E + E, E E, E / E and E * E? Then it would suddenly be possible to derive strings
like
5 + 2 * 3
which should be derived to5 + (2 * 3) = 11
and not(5 + 2) * 3 = 21
as it would if we always placed the parentheses to the left.
Ok, so we can now assume that the grammar for our programming language is un-ambiguous
but that still leaves us with the major problem of the derivation process being non-deterministic,
something that is highly undesirable for a computer algorithm. Lets tackle that question
by looking at how the kind of parser that well use works.
The parser we will use is called a "LR(1)-parser" which stands for "Left-to-right
parse, Rightmost derivation, 1-symbol look-ahead". The meaning of this will become
clearer in a moment. Another thing I should mention before we begin is that we will
expand our grammar with a new production and a new start symbol S:
S -> S$
The token $ is an end-of-file marker so what the new start symbol and production
does is really to add such a marker to the end of our program. Well need the end-of-file
marker when we parse our program.
Ok, another thing to notice is that we do not start with the start symbol and then
try to derive the program from that we start with what we have, namely the
program, and tries to create the parse tree from the bottom up and end up with the
start symbol. If we can do this we could do the exact same operations in reversed
order to derive the program from the start symbol, right?
Ok, so the parser has a stack and an input stream and
at each step of the parsing it can do one of two things:
Rule 1 is called shifting because it moves data from the input to the
stack and rule 2 is called reducing because it reduces a right side
of a production to a left side. Note that after a reduce there will be the same
number or less terminal symbols on the stack and the same number or
more nonterminal symbols on the stack. This is because there can only be
nonterminals on the left side of a production, right? Make sure you understand this
small paragraph before you go on. When will there be less terminal symbols on the
stack after a reduce? When will there be more nonterminal symbols on the stack after
a reduce?
When the parser shifts the end-of-file marker $ to the stack it accepts the
input and ends successfully.
Ok, lets go back to our original example and take a look at how to shift/reduce parse
the string id = num; id = id + num which
was the very first example I used in this chapter:
|
Stack |
Input stream |
Action |
|
id = num; id = id + num$ |
shift |
|
|
id |
= num; id = id + num$ |
shift |
|
id = |
num ; id = id + num$ |
shift |
|
id = num |
; id = id + num $ |
reduce : E -> num |
|
id = E |
; id = id + num$ |
reduce : S -> id = E |
|
S |
; id = id + num$ |
shift |
|
S ; |
id = id + num$ |
shift |
|
S ; id |
= id + num$ |
shift(*) |
|
S ; id = |
id + num$ |
shift |
|
S ; id = id |
+ num$ |
reduce : E -> id |
|
S ; id = E |
+ num$ |
shift(*) |
|
S ; id = E + |
num$ |
shift |
|
S ; id = E + num |
$ |
reduce : E -> num |
|
S ; id = E + E |
$ |
reduce : E -> E + E |
|
S ; id = E |
$ |
reduce : S -> id = E |
|
S ; S |
$ |
reduce : S -> S ; S |
|
S |
$ |
shift & accept |
This example shows very clearly that shift/reduce parsing is a non-deterministic process!
It was only due to my wise choosing of actions that we were able to correctly parse
the input stream. At multiple points I had a choice of whether to shift or to reduce.
At the first * I could have chosen to reduce id to E and if I had done that the parsing
would have failed. At the second * I had a situation where we had earlier reduced
on the exact same stack top but where it would have been terribly wrong in this case!
So how does a parser know whether to shift or reduce? This is where the '1-symbol
look-ahead' comes into the picture. It refers to that the parser is allowed to "cheat"
and take a look at the next symbol in the input stream and make its choice based on
what it sees there.
If given an un-ambiguous grammar and the ability to look 1 symbol ahead then one can
create a so called parse table which will deterministically tell
you which action to use at each step in the parsing!!
The creation of such a parse table is seriously complicated and I will
not even begin to explain it here. The important thing to know is that this is
what happens inside bison when we gives it a grammar it creates such a parse
table for us and uses it to deterministically parse the program.
I think this should be motivation enough for using bison and never even consider writing
your own parser ;)
Hmm... I see a problem here! Using these rules we can only chose either to
have a function or to have a program in our script collection. What we really
want is to be able to say that a script collection can expand to a list of
programs and functions.
We need a common name for these two phenomena, so lets define a toplevel to
be either a function or a program. We can now say that a scriptcollection can extend
to a list of toplevels. We create the list abstraction like this:
Ok, it is clear that we are going to have a lot of productions with the same nonterminal on the left side. So well introduce a new notation:
S -> T
S -> Q
is now the same as:
S -> T | Q
meaning that S can expand to either T or Q.
Applying this notation we get the following rules for the toplevels:
But this is still not quite correct. We have a problem and that is that we cannot have an empty list! We also need to be able to have empty productions. The final version of the toplevel productions looks like this (and also allows for scriptcollections with no toplevels).
The prefix ne to any nonterminal in PxdScript means non-empty. This is the
way we will be creating lists in the pxdscript grammar (and we will do that in a number
of places so make sure you understand this grammar construct).
Now that we have the toplevels taken care of we simply continue to gradually work
our way down the programs and functions by introducing more and more abstractions
until we reach a certain point where we no longer need more nonterminals to describe
the productions. For example we can start by looking at the function nonterminal -
clearly that is not a good enough description of what a function is. So we introduce
a bunch of production rules to classify what exactly a function is in our program.
I will not try to explain every single detail about the design of PxdScript - it's
better that you spend some time looking through the source code to understand the
grammar and structure of the AST in your own pace. Be prepared to spend a few hours
before you understand it all! This part is arguably the hardest part of the whole
series so don't feel bad if you feel like you don't understand a thing after your
first glance over the grammar file. If you dedicate enough hours to understanding
this stuff then I'm sure you'll get it eventually and then you'll enjoy the very satisfying
feeling of having mastered something truly complicated :)
The AST is a little different from the parse tree in the sense that sometimes it is
tied together with linked lists rather than mother-child relations. This is because
it is impossible to know how many children certain nodes can have. The number of children
to the scriptcollection node for example is equal to the number of programs and functions
the user writes. Thus the AST structure (just for the toplevels) is better described
like this :
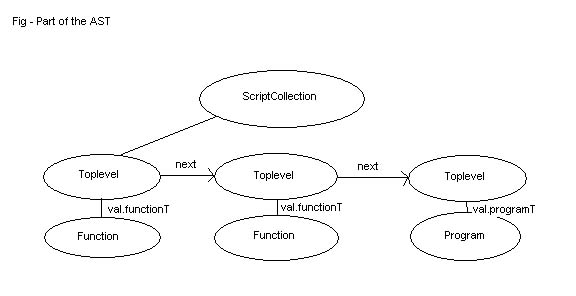
The actual nodes in the tree are defined as structures in the tree.h file which is included in the zip file referred to at the top of this page. The structures for the toplevels looks like this:
typedef struct SCRIPTCOLLECTION{
int lineno;
struct TOPLEVEL *toplevels; /* Linked list of
the toplevels in this script collection */
struct SymbolTable
/* symbol check (later chapter) */
} SCRIPTCOLLECTION;
typedef struct TOPLEVEL {
int lineno;
enum {functionK, programK} kind; /* what
kind of toplevel is this? Function or program? */
union {
struct FUNCTION *functionT;
struct PROGRAM *programT;
} val;
/* The 'val' union allows access to the function or program */
struct TOPLEVEL *next;
/* Pointer to the next toplevel in the linked list */
} TOPLEVEL;
This is the way almost all nodes in the AST will look. They have a lineno variable
for registering where in the source the node belongs. This is used for error reporting
(so we can write for example "The function 'myfunc' at line 236 has already been defined"
or something like that).
Then most of them have a kind enumeration to distinguish between different
kinds of the node. If the nodes has a kind field they will most likely also have a
corresponding data field inside the val union. For example, if the toplevel
is a function its kind will be set to functionK and the val.functionT field will be
a pointer to the function node.
And finally those nodes, which can have a variable number of siblings, will have a next pointer
to the first sibling.
There is A LOT of nodes, each corresponding to different abstractions in the
programming language. I will list the names of each along with a short description
of their purpose, but it is up to you to study the tree.h file to understand the overall
structure of the tree it is too complex to explain in detail here (or rather, it's
not more complex that what I've described already about the toplevels - but there
are so many of them and I'm too lazy to explain them all)..
Ok, so the structure of the AST is defined by the structs in tree.h. Now we need to build it from the source code. We use bison and flex to do this flex scans the source and gives bison the tokens one by one, bison then checks if they are appearing in a legal order.
Phew, that was a lot of theory! Lets see if we can use some of it to actually get some code done for our compiler. So our task at hand is to design an un-ambiguous grammar for our programming language and write that in a format that bison can understand so it can create a shift/reduce parser for us.
What Im going to do is to show you the lang.y file and comment as we step through it:
/* bison file for pxdscript
*
* history:
*/
%{
/* -*** Includes ***-------------------------------------------------------------
*/
#include <stdio.h>
#include <string.h>
#include <malloc.h>
#include "error.h"
#include "tree.h"
/* Prototype for the lexer (no .h file is generated): */
int yylex();
/* Outmost container */
extern SCRIPTCOLLECTION *thescriptcollection;
%}
As you can see a bison file begins much like a flex file with a section where you can add C-code for including header files, defining variable etc. Three important things happens here: First of all we include tree.h which is the header file defining all the structs we use to represent the nodes in out AST. This is to allow us to build the AST from within the bison file. The second important thing is that we define a prototype for a function which can be found in the c code Flex generated for us in the previous chapter. This function returns the next token from the source file and bison use this function to read in new tokens when it needs them. Finally we declare an extern variable 'thescriptcollection'. This is the root of our AST and we do the actual declaration in main.c. When we are done parsing the source file our compiler will access the AST through this variable when it needs to do some analysis like type checking etc.
%start scriptcollection
The line above is defining our 'start symbol' as described in the text above. In other words this is the first nonterminal we will try to expand into a valid program.
%union {
struct SCRIPTCOLLECTION *scriptcollection; /* A collection of functions
and programs.. */
struct TOPLEVEL *toplevel;
struct FUNCTION *function;
/* A standard C-style function */
struct PROGRAM *program;
/* Equals an u1 script program */
struct TRIGGER *trigger;
struct TYPE *type;
struct IDENTIFIER *identifiers;
struct EXP *exp;
struct DECL *decl;
struct FORINIT *forinit;
struct STM *stm;
struct LVALUE *lvalue; int modifier;
/* ModifierKind modifier; */
int entitykind;
/* EntityKind entitykind; */
char *identifier;
int intconst;
int boolconst;
char *stringconst;
};
The union above is very special. It defines the types of the productions.
This isn't something we discussed when we talked about context free grammars above
but in a bison file nonterminals have types. It's quite logical that they do however
- remember that it is exactly the nonterminals which makes up the nodes in our AST.
When talking theory it's fine just to think of nodes in the tree as 'nodes' but when
it finally comes down to some real C programming we need to define data structures
for all the nodes. The union is read like this: We declare a type called 'scriptcollection'
to be a pointer to a SCRIPTCOLLECTION structure, a type called 'toplevel' as a pointer
to a TOPLEVEL structure, a type 'intconst' to be an integer and so on.
/* Token definitions */
%token
tAND tBOOL tCONST tELSE tEQUALS tGEQUALS tIF tINT tLEQUALS tNEQUALS tOR tRETURN
tPROGRAM tSTRING tVOID tWHILE tERROR tFOR tTRIGGERONINIT tTRIGGERONCLICK tTRIGGERONCOLLIDE
tTRIGGERONPICKUP tSETINT tSLEEP tENTITYMDL tENTITYPARTICLE tENTITYPLAYER tENTITYLIGHT
tENTITYCAMERA
Recognize these from the previous chapter? This is where all those tokens were defined that we made Flex return! This is the list of terminal symbols in our language.
%token <identifier> tIDENTIFIER
Some of the terminal symbols needs to contain an actual value. This is the case for the symbols representing constants and variables because at some point we need to go back from a token representation to the actual value of the tokens. The type of this value is defined in the union above so (not surprisingly) the tIDENTIFIER terminal contains a char pointer and the tINTCONST an integer value etc.
%type <scriptcollection> scriptcollection
%type <toplevel> toplevels netoplevels toplevel
%type <function> function
%type <program> program
%type <trigger> trigger
%type <type> type
%type <identifiers> identifiers
%type <exp> initialization exp unaryexp unarypostfixexp exps neexps
%type <decl> decl simpledecl formals neformals formal
%type <forinit> forinits neforinits forinit
%type <stm> nestms stm compoundstm
%type <lvalue> lvalue
%type <modifier> modifier
%type <entitykind> entitytype
The lines above defines the types of the different nonterminals - or in other words the types of the nodes in the AST. Note that the types used are exactly those we defined in the union above! So the nonterminal 'toplevels' are assigned the type 'toplevel' which we in turn defined to be a pointer to a TOPLEVEL structure in the union. As with the tokens that required types the type is written within a pair of < > bracers before the name.
/* Resolve dangling else conflict: */
%left ')'
%left tELSE
/* Resolve binary operator conflicts: */
%left
'=' %left tOR tAND
%left tEQUALS tNEQUALS tLEQUALS tGEQUALS '<' '>'
%left '+' '-'
%left '*' '/'
%left '%'
The lines above are so-called precedence directives. For some reason the lines
listed LAST has the highest precedence! So what they say is that % (modulo) has the
highest precedence when evaluating arithmetic expressions, then comes * and / and
so on. The lowest precedence is assigned to '=' - the assignment. This is logical
- we want to evaluate as much of the right hand side of an assignment before storing
the calculated value to the variable. At this point it is unclear what the precedence
for tELSE and ) is used for - but more on this in a second.
The precedence directives are needed to resolve so-called 'shift/reduce' and
'reduce/reduce' conflicts which arise because the grammar is not un-ambiguous
in its native form. With these precedence rules bison can automatically rewrite the
grammar to produce an un-ambiguous one (as mentioned loosely somewhere above). An
easy example on a shift/reduce conflict is when the parser is trying to parse the
expression E + E + E. After it has shifted E + E onto the stack it will see a '+'
as the next symbol on the input (remember it has a 1 symbol look-ahead) and now it
will have two options to continue - it can either reduce the E + E it already has
on the stack to just a single E and then shift the remaining '+ E' onto the
stack (and reduce again) or it can shift the symbols right away to have 'E + E + E'
on the stack and then reduce twice in a row. The %left precedence directive
favors reducing (and thus it will result in trees like a) in the picture above). You
could also have written %right to favor shifting but then you would run into
problems with the parentheses as described above.
The 'dangling else conflict' is a famous and very well known conflict. The
short version goes like this: In many programs you can write:
if a then if b then s1 else s2
which can be understood in two ways:
if a then {
if b then
s1;
else
s2;
}
if a then {
if b then
s1;
}
else
s2;
In most programming languages '1' is the correct way so that's also how we'll understand the line in PxdScript. There will be a shift/reduce error in bison though - shifting will result in '2' while reducing leads to '1'. Instead of manually rewriting the grammar I have chosen to resolve the conflict with the two more cryptic precedence directives above (the ones for 'tELSE' and ')' ). That is a matter of personal taste though.
%% /* productions */
scriptcollection : toplevels
{ thescriptcollection = makeSCRIPTCOLLECTION($1); }
;
toplevels : /* empty */
{$$ = NULL;}
| netoplevels
{$$ = $1;}
;
netoplevels : toplevel
{$$ = $1;}
| toplevel netoplevels
{$$ = $1; $$->next
= $2;}
;
toplevel : function
{$$ = makeTOPLEVELfunction($1);}
| program
{$$ = makeTOPLEVELprogram($1);}
;
Well, finally we made it to the actual production rules! Above you can see the 4 production
rules I chose to present you with in the section on designing the language. Like in
Flex there is a c-code section for each production rule which is where we actually
build up the AST.
In Flex the c-code were executed when the regular expression were matched by a token
in the source file. In bison the code is executed when the shift/reduce parser
chooses to reduce, using that rule!! It's important that you understand when this
code is executed - it is NOT executed when the tokens are shifted onto the stack,
only when a bunch of tokens already on the stack is reduced to the nonterminal appearing
to the left on the production. So the c-code for the 'scriptcollection -> toplevels'
rule is the very last piece of c-code executed during parsing, right? And what does
that code do? It creates a SCRIPTCOLLECTION node and assigns it to the 'thescriptcollection'
variable - giving us a handle to the root of the AST.
There are certain build-in variables available in bison. '$$' is a variable
referring to the left hand nonterminal in a production. The type of $$ is thus dependant
on what you defined the nonterminals type to be in the union above. For example, take
a look at the 'toplevels' production. In the case of the empty production the 'toplevels'
variable is assigned NULL. In the 'toplevel->function' production the toplevel
is assigned the result of the 'makeTOPLEVELfunction' function call etc. The variables $1,$2,$3 etc
refers to the first, second, third etc symbol on the right side in the production.
All the 'makeTOPLEVELfunction' and similar functions are defined in tree.c and
all they do is to create and initialize the nodes of the AST. 'makeTOPLEVELfunction'
creates and initializes a TOPLEVEL structure and sets its 'kind' member to 'functionK'
for example. As parameter it takes $1 - and what is that? It's the first symbol
of the right side of the production: in this case it is the function nonterminal.
The type of a function nonterminal is 'FUNCTION*' so the argument that the
C-function makeTOPLEVELfunction gets is a pointer to the function this toplevel
represents.
Notice how this implies a recursive building of the AST - the root node 'thescriptcollection'
is assigned the result of a function taking $1 as parameter. But what is $1?
That is the result returned by the 'toplevels' production which in turn is dependant
on the 'function' and 'program' production which is dependant on other productions
etc.
When $1 is finally ready to be passed to makeSCRIPTCOLLECTION it is
actually a whole tree which has been build from the productions deeper in the recursion.
Finally notice how the linked lists are build up by first recursing on the single
element in the production and then linking that elements 'next' pointer to the result
of parsing the rest of the list.
I won't go into detail with the rest of the productions but brew a big can of coffee
and spend a few hours trying to get a hold on the structure of the AST and the rest
of the grammar. Just remember that what we are doing is gradually recursing deeper
and deeper into the program source and building up the AST from the bottom and up
and you'll be fine.
decl : type identifiers initialization ';'
{$$ = makeDECLvariable(noneMod,$1,$2,$3);}
| modifier type identifiers initialization ';'
{$$ = makeDECLvariable($1,$2,$3,$4);}
;
simpledecl : type tIDENTIFIER initialization
{$$ = makeDECLsimplevar($1,$2,$3);}
;
modifier : tCONST
{$$ = constMod;}
;
identifiers : tIDENTIFIER
{$$
= makeIDENTIFIER($1);}
| tIDENTIFIER ','
identifiers
{$$ = makeIDENTIFIER($1);
$$->next = $3;}
;
initialization : /* empty */
{$$ = NULL;}
|
'=' exp {$$ = $2;}
;
type : tINT
{$$ = makeTYPEint();}
| tBOOL
{$$ = makeTYPEbool();}
| tSTRING
{$$ = makeTYPEstring();}
;
function : type tIDENTIFIER '(' formals ')' compoundstm
{$$ = makeFUNCTION($2,$1,$4,$6);}
| tVOID tIDENTIFIER '(' formals ')' compoundstm
{$$ = makeFUNCTION($2, makeTYPEvoid(),
$4, $6);}
;
formals : /* empty */
{$$ = NULL;}
| neformals
{$$ = $1;}
;
neformals : formal
{$$ = $1};
| formal ',' neformals
{$$ = $1; $$->next
= $3;}
;
formal : type tIDENTIFIER
{$$ = makeDECLformal($1,$2);}
;
trigger : tTRIGGERONCLICK '(' tSTRINGCONST ')'
{ $$ = makeTRIGGERonclick($3);
}
| tTRIGGERONCOLLIDE '(' tSTRINGCONST
')'
{ $$ = makeTRIGGERoncollide($3);
}
| tTRIGGERONPICKUP '(' tSTRINGCONST ')'
{ $$ = makeTRIGGERonpickup($3);
}
| tTRIGGERONINIT { $$ = makeTRIGGERoninit();
}
;
program : tPROGRAM tIDENTIFIER trigger compoundstm
{$$ = makePROGRAM($2,$3,$4);}
;
compoundstm : '{' '}'
{$$
= NULL;}
| '{' nestms '}'
{$$
= $2;}
;
nestms : stm
{$$ = $1;}
| nestms stm
{$$ = makeSTMsequence($1,$2);}
;
entitytype : tENTITYMDL
{$$ = mdlEntity;}
| tENTITYPARTICLE
{$$ = particleEntity;}
| tENTITYPLAYER
{$$
= playerEntity;}
| tENTITYLIGHT
{$$ = lightEntity;}
| tENTITYCAMERA
{$$ = cameraEntity;}
;
stm : ';'
{$$ = makeSTMskip();}
| tRETURN ';'
{$$ = makeSTMreturn(NULL);}
| tRETURN exp ';'
{$$ = makeSTMreturn($2);}
| tIF '(' exp ')' stm
{$$ = makeSTMif($3,makeSTMscope($5));}
| tIF '(' exp ')' stm tELSE stm
{$$ = makeSTMifelse($3,makeSTMscope($5),makeSTMscope($7));}
| tWHILE '(' exp ')' stm
{$$ = makeSTMwhile($3,$5);}
| tFOR '(' forinits ';' exp ';' exps ')' stm
{$$ = makeSTMfor($3,$5,$7,makeSTMscope($9));}
| compoundstm
{$$ = makeSTMscope($1);}
| decl
{$$ = makeSTMdecl($1);}
| exp ';'
{$$ = makeSTMexp($1);}
| tSLEEP '(' exp ')'
{$$ = makeSTMsleep($3);}
| tSLEEP '(' ')'
{$$ = makeSTMsleep(NULL);}
/* sleep until re-triggered */
| tSETINT '(' entitytype ',' exp ',' exp ',' exp ')'
/* Interface between script and game ! */
{$$ = makeSTMsetint($3, $5, $7, $9);}
;
forinits : /* empty */
{$$ = NULL;}
| neforinits
{$$ = $1;}
;
neforinits : forinit
{$$ = $1;}
| forinit ',' neforinits
{$$ = $1;
$$->next = $3;}
;
forinit : simpledecl
{$$ = makeFORINITdecl($1);}
| exp
{$$ = makeFORINITexp($1);}
;
exp : lvalue '=' exp
{$$ = makeEXPassignment($1,$3);}
| exp tEQUALS exp
{$$ = makeEXPequals($1,$3);}
| exp tNEQUALS exp
{$$ = makeEXPnequals($1,$3);}
| exp '<' exp
{$$ = makeEXPless($1,$3);}
| exp '>' exp
{$$ = makeEXPgreater($1,$3);}
| exp tLEQUALS exp
{$$ = makeEXPlequals($1,$3);}
| exp tGEQUALS exp
{$$ = makeEXPgequals($1,$3);}
| exp '+' exp
{$$ = makeEXPplus($1,$3);}
| exp '-' exp
{$$ = makeEXPminus($1,$3);}
| exp '*' exp
{$$ = makeEXPmult($1,$3);}
| exp '/' exp
{$$ = makeEXPdiv($1,$3);}
| exp '%' exp
{$$ = makeEXPmodulo($1,$3);}
| exp tAND exp
{$$ = makeEXPand($1,$3);}
| exp tOR exp
{$$ = makeEXPor($1,$3);}
| unaryexp {$$ = $1;}
;
unaryexp : '-' unaryexp
{$$ = makeEXPuminus($2);}
| '!' unaryexp
{$$ = makeEXPnot($2);}
| '(' type ')' unaryexp
{$$ = makeEXPcast($2,$4);}
| unarypostfixexp
{$$ = $1;}
;
unarypostfixexp : tINTCONST
{$$ = makeEXPintconst($1);}
|
tBOOLCONST
{$$ = makeEXPboolconst($1);}
| tSTRINGCONST
{$$ = makeEXPstringconst($1);}
| lvalue
{$$ = makeEXPlvalue($1);}
| '(' exp ')'
{$$ = $2;}
| tIDENTIFIER '(' exps ')' /* Invokation */
{$$ = makeEXPinvoke($1,$3);}
;
exps : /* empty */
{$$ = NULL;}
| neexps
{$$ = $1;}
;
neexps : exp
{$$ = $1;}
| exp ',' neexps
{$$ = $1; $$->next = $3;}
;
lvalue : tIDENTIFIER
{$$ = makeLVALUEid($1);}
;
Ok, somehow I get the feeling that some of you might still not be 100% certain about how to actually combine what you have learned so far into an executable actually doing something useful. So to sum up what we have achieved now:
From now on we are going to work with this tree to analyze the data in it. We do so by making multiple recursions through the tree, simply starting with the root node and then recursing on each non-leaf. To give you an example of how we are going to do that I have included a phase called 'pretty-printing' with the source code for this chapter.
The idea behind pretty-printing is to take an AST and write it back to the screen as source code again. This sounds meaningless but it is actually a useful way to see that one has indeed parsed the source file correctly into the AST. Nothing hard is going on in the pretty-printing step so I won't explain it here, just browse through the source and try to learn the overall structure of the tree. Don't worry if you never learn it all by heart - I still use tree.h as reference when I make changes to the code ;)
So what's our total status this time? How far have we progressed? Well, pretty far - now we will only accept programs where the tokens appear in a legal order. There is still a lot to do though - the compiler will happily accept calls to non-existent functions, you can refer variables before they are defined, assign a string to an integer variable etc etc. But we'll take care of this in later chapters.
So, still with me? I sure hope so because from now on it is going to be a lot easier.
This was the main hurdle to overcome both for you and for me and I hope that I explained
things well enough because I know this isn't easy stuff.
But fool around with the source code and spend some time understanding what's going
on and expand the language to fit your specific needs! The sooner you do this the
better because the later you make changes the more painful they will be.
Now will be a good time to credit a few people who has helped writing some code that
the front-end of this compiler is based upon. Here I'm thinking especially on my study
group from the university with whom I originally created my first compiler - namely
Carsten Kjaer and Mads Olesen. They have kindly agreed to let me reuse some of the
code we made back then in this compiler (remember I told you that much of a compilers
code could be reused in every compiler). Also thanks to Michael I. Schwartzbach who
originally taught me all this stuff as well as provided us with some of the
source we used in our first compiler. See you around for the next chapter soon.
Keep on codin'
Kasper Fauerby
www.peroxide.dk